03. 排序算法

一、是什么、区别：

排序是程序开发中非常常见的操作，对一组任意的数据元素经过排序操作后，就可以把他们变成一组一定规则排序的有序序列

排序算法属于算法中的一种，而且是覆盖范围极小的一种，彻底掌握排序算法对程序开发是有很大的帮助的

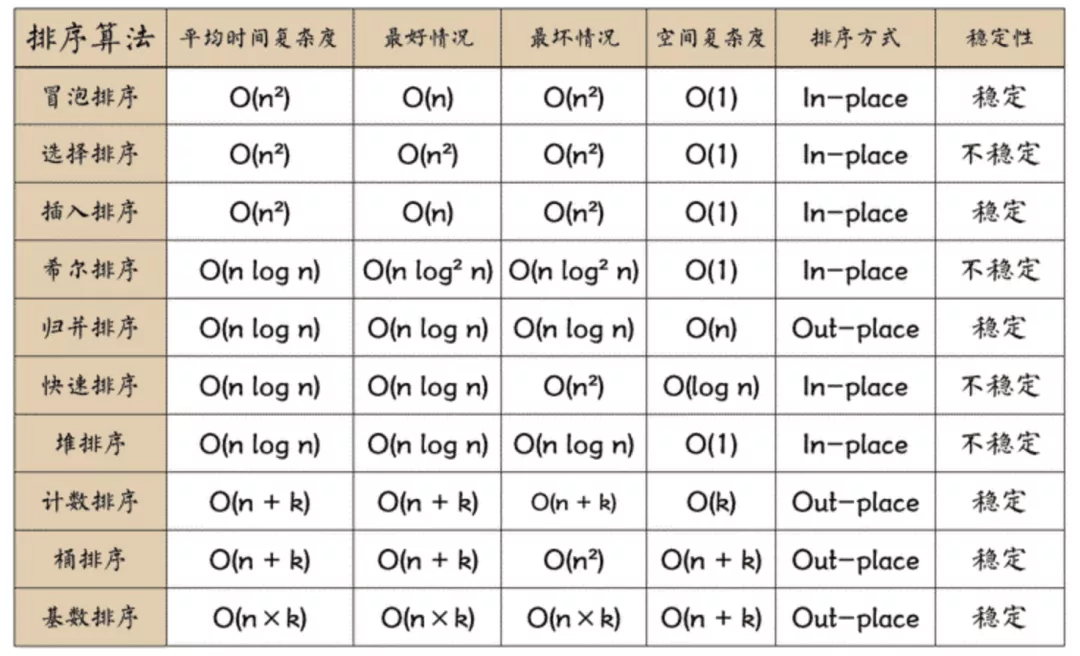
对于排序算法的好坏衡量，主要是从时间复杂度、空间复杂度、稳定性

时间复杂度、空间复杂度前面已经讲过，这里主要看看稳定性的定义

稳定性指的是假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变

即在原序列中，r[i] = r[j]，且 r[i] 在 r[j] 之前，而在排序后的序列中，r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。

二、选择排序：

定义：

​ 选择排序是一种简单直观的排序算法，无论什么数据进行排序都是O（n2）的时间复杂度，其存在不稳定性，不建议排序复杂的数据，所以用到它时，数据规模越小越好。

原理：

​ 首先在未排序数列中找到最小（或最大）元素，将其存放到数列的起始位置，然后再从剩余未排序的元素中继续寻找最小（或最大）元素，然后放到已排序序列的末尾。

​ 以此类推，直到所有元素排序完毕。

代码实现：

// 选择排序。
function selectionSort(arr) {
	if(arr === null || arr.length === 1 ) return arr;

	for (let i = 0; i < arr.length; i++) {
		let minIndex = i;
		for (let k = i + 1; k < arr.length; k++) {
			// 保存最小的数。
			if (arr[k] < arr[minIndex]) minIndex = k;
		};

		let temp = arr[i];
		arr[i] = arr[minIndex];
		arr[minIndex] = temp;
	};
	return arr;
};

三、冒泡排序：

定义：

​ 冒泡排序的思想就是在每次遍历一遍未排序的数列之后，将一个数据元素浮上去（也就是排好了一个数据）。

​ 时间复杂度高。

原理：

​ 首先比较相邻元素，当第一个元素大于第二个元素，则交换元素位置。

​ 针对每一个相邻元素重复比对，直到数列结尾，这样，最后的元素是最大数。

​ 针对所有的元素重复以上步骤，除了最后一个。

​ 每次对越来越少的元素重复以上步骤，直到没有任何一对数字需要比较。

代码实现：

// 冒泡排序。
function bubbleSort(arr) {
	if(arr === null || arr.length === 1 ) return arr;

	for (let i = 0; i < arr.length; i++) {
		for (let k = 0; k < arr.length - 1 - i; k++) {
			// 相邻两个元素比对。
			if (arr[k] > arr[k + 1]) {
				let temp = arr[k];
				arr[k] = arr[k + 1];
				arr[k + 1] = temp;
			};
		};
	};
	return arr;
};

三、插入排序：

定义：

​ 其主要的实现思想是将数据按照一定的顺序一个一个的插入到有序的表中，最终得到的序列就是已经排序好的数据。

原理：

​ 通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入元素。

代码实现：

// 插入排序。
function insertionSort(arr) {
	if (arr === null || arr.length === 1) return arr;

	for (let i = 1; i < arr.length; i++) {
		for (let k = i - 1; k >= 0 && arr[k] > arr[k + 1]; k--) {
			let temp = arr[k];
			arr[k] = arr[k + 1];
			arr[k + 1] = temp;
		};
	};
	return arr;
};

四、归并排序：

定义：

​ 排序一个数组，我们先把数组从分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

​ 归并排序采用的是分治思想。

​ 分治：：顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。

原理：

分：把数组分成两半，再递归对子数组进行分操作，直至到一个个单独数字

合：把两个数合成有序数组，再对有序数组进行合并操作，直到全部子数组合成一个完整的数组

代码实现：

class MergeSort {
	constructor(arr) {
		this.arr = arr;
		this._mergeSort(this.arr);
	};

	// 归并排序。
	_mergeSort(arr) {
		if (arr === null || arr.length < 2) return arr;
		this.arr = this._process(arr, 0, arr.length);
	};

	// 拆分。
	_process(arr) {
		const len = arr.length;
		if (len === 1) return arr;
		let mid = Math.floor(len / 2);
		// 拆分数组。
		let left = arr.slice(0, mid);
		let right = arr.slice(mid);

		return this._merge(this._process(left), this._process(right));
	};

	// 合并。
	_merge(left, right) {
		let result = [];

		while (left.length && right.length) {
			if (left[0] <= right[0]) {
				result.push(left.shift());
			} else {
				result.push(right.shift());
			};
		};

		while (left.length) {
			result.push(left.shift());
		};

		while (right.length) {
			result.push(right.shift());
		};

		return result;
	};
};